
|

|

|

|
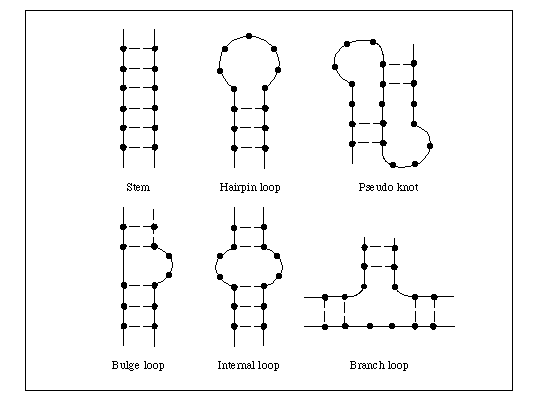
一本鎖RNAの二次構造は相補的な配列が局所的に二重らせん構造をとることにより形成される。二重らせん部分をステムといい、ステムをつなぐ一本鎖の部分がループである。ループにはヘアピンループ、インターナルループ、バルジループ、ブランチループといった区別がある(図)。RNA二次構造予測は、ステム構造と各ループ構造の安定性の評価値を合計したエネルギー関数を最小化することにより行われる。従って、評価関数は異なるが基本的にRNA二次構造予測の問題は配列の最適アライメントの問題である。解法は大きく2種類あり、1つはダイナミックプログラミング法により配列の自分自身との最適アライメントを探す方法、もう1つはまずステムの候補を作りその最適組合せを探す方法である。前者は厳密な最適解およびその近傍の局所解を探すことに、後者は構造的に大きく異なる局所解を多数探すことに向いている。
第1のダイナミックプログラミング法のアルゴリズムは
で表現される。ここで、αi,j はベースペア i, j とその前のベースペアによるステム部分のエネルギー値である。これがベースペア単位ではなく、連続した2つのベースペア単位に割り当てられるのは、二重らせんを安定化させるベーススタッキングの効果を取り入れるためである。ベースペアとしては A-U、G-C 以外に G-U も考慮される。βk, γk, εk, δk はそれぞれ長さ k のバルジループ、インターナルループ、ブランチループ、ヘアピンループのエネルギー値である。バルジループはどちらの鎖に入るかで2つの可能性がある。εk を含む項は遠距離相互作用で配列上離れた部分を近接させる効果である。なおこのアルゴリズムは、2つの配列のアライメントで一般的な長さ依存のギャップペナルティを入れた場合と同様に、O (n3) のアルゴリズムである。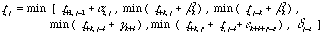
エネルギー値は熱力学的な実験データなどからパラメタ化されているが、これには曖昧性があり、またその単純和としてのエネルギー関数がどの程度適切か不明なことから、数学的な最小エネルギーが常に生物的に意味のある構造とは言えない。そのため、実験的に既知の二次構造情報を制約条件として入れたり、最小値から与えられた範囲内にある局所最適解を探したり、ダイナミックプログラミング法の改良が行われている。ダイナミックプログラミング法は数学的に厳密な方法であるため、局所最適解をある範囲内で探そうとすると、そのすべてを得ることができる。しかしこれは必ずしも望ましいことではない。RNA二次構造のエネルギー関数では(恐らく他の最適化問題の評価関数でも)、エネルギー曲面に無数の細かいでこぼこがあり、その1つ1つを局所最適解として捕らえるのではなく、何らかの形でエネルギー曲面のスムージングを行って大域的な意味での局所最適解を見いだす必要がある。すなわち、構造的にほとんど大差ない局所最適解を探すのではなく、構造的に大きく異なる局所最適解を探すのである。これにはステム部分の組合せを行う第2のアプローチが有効である。